문제
- 문제 링크
BOJ 28073 - PSAT 특별과정
PSAT 특별과정의 구조가 그래프 형태로 주어진다.
각 노드마다 알파벳이 메겨져 있고, 시작 위치와 종료 위치는 특정 조건에서만 성립될 수 있다.
임의의 시작 위치에서 임의의 종료 위치에 도달할 때까지 지나온 노드들을 이어 붙이면 하나의 문자열을 완성 시킬 수 있다.
이때, 가장 짧고 사전 상 가장 앞선 문자열을 만들어내도록 하는 경로를 구해보자.
TL : $2$ sec, ML : $512$ MB
$2 ≤ N ≤ 10^6$ $0 ≤ M ≤ min(10^6, N*(N-1) / 2)$ 등장하는 알파벳은 전부 대문자이며, 시작 문자 $S$와 종료 문자 $E$는 같은 문자일 수 있다.
알고리즘 분류
- 그래프 이론(graphs)
- 그래프 탐색(graph_traversal)
- 너비 우선 탐색(bfs)
- 정렬(sorting)
풀이
이 문제에 만약 다음의 조건이 추가 됐다고 생각해보자.
이는 시작 노드부터 $BFS$를 진행하면서, 매 순간마다 인접 노드들을 알파벳 순으로 정렬해주고 순회 하면 쉽게 해결할 수 있다.
하지만 위 조건이 없으니, 같은 알파벳을 지닌 인접 노드를 방문하는 순서에 따라 답이 달라지게 된다.
따라서 추가적인 작업을 통해 위 상황을 유도해야 한다.
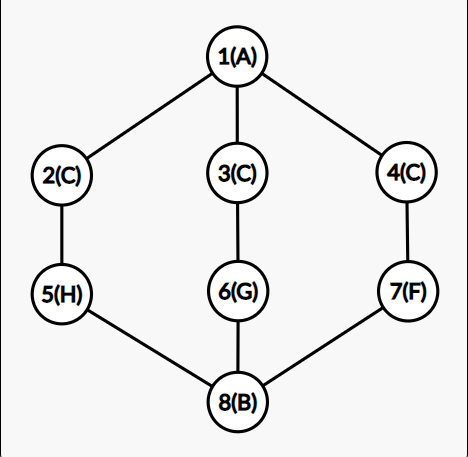
구체적으로 위와 같은 문제 상황에서 아래처럼 만들어주는 작업이 필요하다는 것이다.
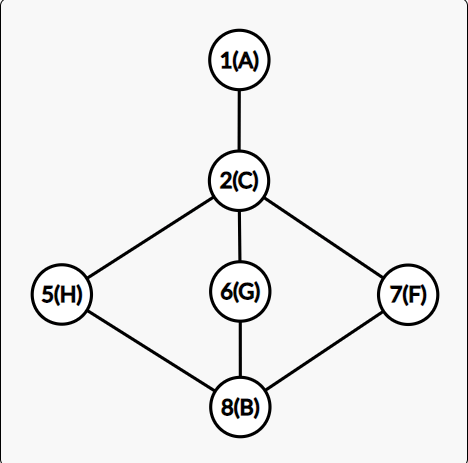
나는 위 작업을 각 알파벳마다 대표 노드를 정해줌으로써 해결하였다.
자세한 내용은 코드 및 주석을 참고하자.
또 하나 신경 쓸 것으로, 출발점에 대한 기준만 제시 되었을 뿐 한 노드가 특정된 것이 아니다.
도착점 역시 마찬가지다.
이 상황에서도 위의 작업을 적용할 수 있도록 유도해주면 그만이다.
이는 다음의 작업을 통해 일반화를 시킬 수 있다.
$N + 1$번, $N + 2$번 노드를 추가하자. 이는 각각 유일한 출발점, 유일한 도착점이 된다. 시작 문자 $S$가 메겨진 노드들의 집합을 $U_1$, 종료 문자 $E$가 메겨진 노드들의 집합을 $U_2$라 할 때, $N + 1$번 노드에서 집합 $U_1$로 향하는 간선, 집합 $U_2$ 에서 $N + 2$번 노드로 향하는 간선을 세팅하자. 결국 $N + 1$번 노드를 시작으로, 앞서 말한 작업을 통해 모든 과정을 일반화 시킬 수 있다.
노드들의 연결 리스트들을 $merge$하는 과정에서, 중복 삽입이 일어나지 않도록 주의하자.
까딱하면 $MLE$나 $TLE$를 맞기 십상이니 말이다.
이 문제를 시도하는 사람들에게 역추적은 쉬운 문제일테니 이에 관한 설명은 생략 하겠다.
같은 알파벳 노드들에 대응하는 과정에서, 위 작업 말고도 백트래킹을 적절히 이용해도 되는 듯 하다.
또한 역으로 끝점부터 최단 경로들을 파악한 뒤 시작점부터 따라가는 등.. 다양한 좋은 풀이들이 있는 것 같다.
전체 코드
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 | #include<bits/stdc++.h> #define N 1000005 using namespace std; vector <int> Eg[N]; char s, e, a[N]; int n, m, path[N]; void Init() { ios_base::sync_with_stdio(0); cin.tie(0); cin >> n >> m >> s >> e; for (int i(1); i <= n; i++) { cin >> a[i]; if (a[i] == s) Eg[n + 1].push_back(i); // 유일한 시작점 및 도착점의 일반화를 위한 작업 if (a[i] == e) Eg[i].push_back(n + 2); } for (int i, j; m--;) { cin >> i >> j; Eg[i].push_back(j); Eg[j].push_back(i); } } void Solve(queue <int> Q = {}) { bool Visit[N]{}; Visit[n + 1] = 1; // 중복 삽입 방지를 위한 배열 for (Q.push(n + 1); Q.size();) { int rep[101]{}, now(Q.front()); Q.pop(); // rep[x] = y : 알파벳 x의 대표 정점은 y. 알파벳 x가 메겨진 모든 인접 노드들의 인접 리스트는 y의 인접 리스트로 merge된다. sort(Eg[now].begin(), Eg[now].end(), [](int& x, int& y) {return a[x] < a[y]; }); // 인접 노드들에 대해 알파벳 순으로 정렬 for (int& i : Eg[now]) { if (!rep[a[i]] && !path[i]) // 알파벳 a[i]의 대표 노드가 설정되지 않았다면 { Visit[i] = 1, path[i] = now; Q.push(rep[a[i]] = i); // 큐에는 각 알파벳의 대표 노드들만 넣어주면 됨 } if (i ^ rep[a[i]]) // 대표 노드가 아닌 노드의 인접 리스트에 대해, for (int& j : Eg[i]) if (!Visit[j]) // 등장하지 않은 노드들을 Visit[j] = 1, Eg[rep[a[i]]].push_back(j); // 대표 노드의 인접 리스트로 보냄 } } } void End(string an = "") { if (!path[n + 2]) cout << "Aaak!", exit(0); // path[n + 2]가 업데이트 되지 않았다면 조건에 맞는 문자열은 존재하지 않는다. for (int i(path[n + 2]); i ^ (n + 1); i = path[i]) an += a[i]; // path[n + 2]를 시작으로, path[i] ≠ n + 1 인 동안 for (int i(an.size() - 1); !!~i; cout << an[i--]); } int main() { Init(); Solve(); End(); } | cs |
comment
정답을 완성하기까지 꽤 많은 시행 착오가 있었다..
한 번 쯤 겪어봐야 하는 좋은 문제라고 생각한다.
코드가 썩 마음에 들지 않는데 나중에 처음부터 다시 짜봐야겠다.
'Problem Solving > Baekjoon Online Judge (Platinum)' 카테고리의 다른 글
| 백준 4787 - Covered Walkway (C++) (0) | 2023.08.04 |
|---|---|
| 백준 10293 - Ranks in groups (C++) (0) | 2023.07.19 |
| 백준 13028 - 민호의 소원 (C++) (0) | 2023.06.24 |
| 백준 28090 - 특별한 한붓그리기 (C++) (0) | 2023.05.31 |
| 백준 17831 - 대기업 승범이네 (C++) (0) | 2023.05.22 |